Senin, 12 Desember 2011

pengertian trigonometri

Trigonometri

Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi trigonometrik seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.

Hubungan fungsi trigonometri

$\tan A = \frac{\sin A}{\cos A}\,$

$\cot A = \frac{1}{\tan A} = \frac{\cos A}{\sin A}\,$

$\sec A = \frac{1}{\cos A}\,$

Sinus

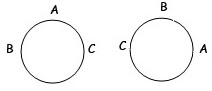
Sinus (lambang: sin; bahasa Inggris: sine) dalam matematika adalah perbandingan sisi segitiga yang ada di depan sudut dengan sisi miring (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o). Perhatikan segitiga di kanan; berdasarkan definisi sinus di atas maka nilai sinus adalah

Nilai sinus sudut istimewa

$\sin 0^o = 0\,$

$\sin 15^o = \frac {\sqrt{6} - \sqrt{2}}{4}\,$

$\sin 30^o = \frac{1}{2}\,$

$\sin 45^o = \frac {\sqrt{2}}{2}\,$

$\sin 60^o = \frac {\sqrt{3}}{2}\,$

$\sin 75^o = \frac {\sqrt{6} + \sqrt{2}}{4}\,$

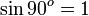
$\sin 90^o = 1\,$

Kosinus

Kosinus atau cosinus (simbol: cos; bahasa Inggris: cosine) dalam matematika adalah perbandingan sisi segitiga yang terletak di sudut dengan sisi miring (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o). Perhatikan segitiga di kanan. Berdasarkan definisi kosinus di atas maka nilai kosinus adalah

$\cos A = {\mbox{b} \over \mbox{c}} \qquad \cos B = {\mbox{a} \over \mbox{c}}$

Nilai kosinus positif di kuadran I dan IV dan negatif di kuadran II dan III.

Tangen

Tangen (lambang tg, tan; bahasa Belanda: tangens; bahasa Inggris: tangent) dalam matematika adalah perbandingan sisi segitiga yang ada di depan sudut dengan sisi segitiga yang terletak di sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o).

Berdasarkan segitiga pada ilustrator (di kanan), berdasarkan definisi tangen, di atas maka nilai tangen adalah

$\tan A = {\mbox{a} \over \mbox{b}} \qquad \tan B = {\mbox{b} \over \mbox{a}}$

Nilai tangen positif di kuadran I dan III dan negatif di kuadran II dan IV.

Sekan

Sekan (lambang: sec; bahasa Inggris: secant) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak pada sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o). Perhatikan segitiga di kanan; berdasarkan definisi sekan di atas maka nilai sekan adalah

$\sec A = {\mbox{c} \over \mbox{b}} \qquad \sec B = {\mbox{c} \over \mbox{a}}$

Hubungan sekan dengan kosinus:

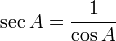
$\sec A = \frac{1}{\cos A}\,$

Kosekan

Kosekan (disimbolkan dengan cosec atau csc; bahasa Inggris: cosecant) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o). Perhatikan segitiga di kanan; berdasarkan definisi kosekan di atas maka nilai kosekan adalah

$\csc A = {\mbox{c} \over \mbox{a}} \qquad \csc B = {\mbox{c} \over \mbox{b}}$

Hubungan kosekan dengan sinus:

Kotangen

Kotangen (lambang: cot, cotg, atau cotan; bahasa Inggris: cotangent) dalam matematika adalah perbandingan sisi segitiga yang terletak pada sudut dengan sisi segitiga yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o). Perhatikan segitiga di kanan; berdasarkan definisi kotangen di atas maka nilai kotangen adalah

$\cot A = {\mbox{b} \over \mbox{a}} \qquad \cot B = {\mbox{a} \over \mbox{b}}$

Hubungan kotangen dengan tangen:

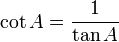
$\cot A = \frac{1}{\tan A}\,$

Sabtu, 03 Desember 2011

PENGERTIAN LINGKARAN (MATEMATIKA XI IPA)

Lingkaran

Elemen lingkaran

Elemen-elemen yang terdapat pada lingkaran, yaitu :

Elemen lingkaran yang berupa titik, yaitu :
1. Titik pusat (P)
  merupakan titik tengah lingkaran, dimana jarak titik tersebut dengan titik manapun pada lingkaran selalu tetap.

Elemen lingkaran yang berupa garisan, yaitu :
1. Jari-jari (R)
  merupakan garis lurus yang menghubungkan titik pusat dengan lingkaran.
2. Tali busur (TB)
  merupakan garis lurus di dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda.
3. Busur (B)
  merupakan garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran.
4. Keliling lingkaran (K)
  merupakan busur terpanjang pada lingkaran.
5. Diameter (D)
  merupakan tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter ini membagi lingkaran sama luas.
6. Apotema
  merupakan garis terpendek antara tali busur dan pusat lingkaran.

Elemen lingkaran yang berupa luasan, yaitu :
1. Juring (J)
  merupakan daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya.
2. Tembereng (T)
  merupakan daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya.
3. Cakram (C)
  merupakan semua daerah yang berada di dalam lingkaran. Luasnya yaitu jari-jari kuadrat dikalikan dengan pi. Cakram merupakan juring terbesar.
Persamaan

Suatu lingkaran memiliki persamaan

$(x - x_0)^2 + (y - y_0)^2 = R^2 \!$

dengan adalah jari-jari lingkaran dan adalah koordinat pusat lingkaran.

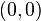Jika pusat lingkaran terdapat di , maka persamaan di atas dapat dituliskan sebagai

$x^2 + y^2 = R^2 \!$

Bentuk persamaan lingkaran dapat dijabarkan juga menjadi bentuk

$x^2 + Ax + y^2 + By + C = 0 \!$

dengan adalah jari-jari lingkaran dan adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.

Persamaan parametrik

Lingkaran dapat pula dirumuskan dalam suatu persamaan parameterik, yaitu

$x = x_0 + R \cos(t) \!$
$y = y_0 + R \sin(t) \!$

yang apabila dibiarkan menjalani t akan dibuat suatu lintasan berbentuk lingkaran dalam ruang x-y.

Luas lingkaran

Luas lingkaran

Luas lingkaran memiliki rumus

$A = \pi R^2 \!$

yang dapat diturunkan dengan melakukan integrasi elemen luas suatu lingkaran

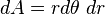
$dA = rd\theta\ dr$

Luas lingkaran dapat dihitung dengan memotong-motongnya sebagai elemen-elemen dari suatu juring untuk kemudian disusun ulang menjadi sebuah persegi panjang yang luasnya dapat dengan mudah dihitung. Dalam gambar r berarti sama dengan R yaitu jari-jari lingkaran.

Luas juring

Luas juring suatu lingkaran dapat dihitung apabila luas lingkaran dijadikan fungsi dari R dan θ, yaitu;

$A(R,\theta) = \frac 1 2 R^2 \theta \!$

dengan batasan nilai θ adalah antara 0 dan 3π. Saat θ bernilai 2π, juring yang dihitung adalah juring terluas, atau luas lingkaran.

Luas cincin lingkaran

Suatu cincin lingkaran memiliki luas yang bergantung pada jari-jari dalam $R_1\!$ dan jari-jari luar $R_2\!$ , yaitu

$A_{cincin} = \pi (R_2^2 - R_1^2) \!$

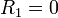di mana untuk $R_1 = 0\!$ rumus ini kembali menjadi rumus luas lingkaran.

Luas potongan cincin lingkaran

Dengan menggabungkan kedua rumus sebelumnya, dapat diperoleh

$A_{potongan\ cincin} = \frac \pi 2 (R_2^2 - R_1^2) \theta \!$

yang merupakan luas sebuah cincin tak utuh.

Keliling lingkaran

Keliling lingkaran memiliki rumus:

$L = 2\pi R\!$

Panjang busur lingkaran

Panjang busur suatu lingkaran dapat dihitung dengan menggunakan rumus

$L = R \theta \!$

yang diturunkan dari rumus untuk menghitung panjang suatu kurva

$dL = \int \sqrt{1 + \left( \frac{dy}{dx}\right) ^2 } dx \!$

di mana digunakan

$y = \pm \sqrt{R^2 - x^2} \!$

sebagai kurva yang membentuk lingkaran. Tanda $\pm$ mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.

π(Pi)

Nilai pi adalah suatu besaran yang merupakan sifat khusus dari lingkaran, yaitu perbandingan dari keliling K dengan diameternya D:

$\pi = \frac K D$

penjelasan peluang

PELUANG BAB II (MATEMATIKA IPA)

Permutasi dan Kombinasi (PELUANG-MATEMATIKA)

PERMUTASI

Coba perhatikan contoh-contoh di bawah untuk memahami Permutasi dalam konsep Peluang pada pelajaran Matematika.

Contoh I:

{a,b,c}

Jika dipilih 2 dari 3 unsur tersebut, maka banyaknya permutasi dari 3 unsur setiap pengambilan 2 unsur adalah 6, yaitu ab, ba, ac, ca, bc, cb.

Ditulis 3P2 = 6.

Contoh II:

{a,b,c}

maka, banyaknya permutasi dari 3 unusr setiap pengambilan 3 unsur adalah 6, yaitu abc, acb, bac, bca, cab, cba.

Ditulis 3P3 = 6

RUMUS

Catatan: Notasi Faktorial

3! = 3x2x1

5! = 5x4x3x2x1

1! = 1

Def 0! = 1

Permutasi Siklis

{a,b,c} Maka, jika menggunakan permutasi siklis, hasil dari pengambilan 3 unsur dari 3 unsur dapat digambarkan seperti gambar di samping.

RUMUS: banyaknya permutasi = (n-1)!

KOMBINASI

Contoh III:

{a,b,c}, pengambilan 2 unsur dari 3 unsur.

menggunakan kombinasi maka akan diperoleh hasil kombinasinya ab, bc, ca.

Ditulis 3C2.

RUMUS

PERBEDAAN KOMBINASI DAN PERMUTASI

Salah satu perbedaan antara Permutasi dan Kombinasi adalah jika Permutasi maka perbedaan urutan menjadikan perbedaan makna, sementara di Kombinasi perbedaan urutan tidak akan menjadikan perbedaan makna. Contoh: {a,b,c} pengambilan 2 unsur dari 3 unsur jika menggunakan permutasi maka akan diperoleh hasil ab, ba, ac, ca, bc, cb.

Tetapi jika menggunakan kombinasi hasil yang diperoleh adalah ab, ca, bc.

Contoh lain permutasi:

ada nomor kendaraan di Indonesia yaitu AB (Jogjakarta dan sekitarnya), tetapi apabila dibalik maka menjadi BA (Padang), maka terlihat perbedaan maknanya.

Contoh lain kombinasi:

Ada dua titik A dan B, dihubungkan oleh satu garis.

Maka garis AB = BA, yang berarti tidak menyebabkan perbedaan makna.

Peluang suatu kejadian (MATEMATIKA - XI IPA)

ISTILAH-ISTILAH DALAM PELUANG

Ruang Sampel

Adalah himpunan semua hasil yang mungkin dari suatu percobaan. Contoh: Pada percobaan pelemparan sebuah dadu, maka ruang sampelnya adalah S={1,2,3,4,5,6}

Kejadian

Adalah himpunan bagian dari ruang sampel. Contoh: Kejadian munculnya mata ganjil pada pelemparan sebuah dadu, A={1,3,5}

Peluang

Peluang suatu kejadian A didefinisikan

N(A) = Banyaknya anggota himpunan A

N(S) = Banyaknya anggota himpunan S

Contoh: Pada pelemparan sebuah dadu, tentukan peluang munculnya mata dadu bilangan prima!

Jawab:

S={1,2,3,4,5,6} N(S)=6

A={2,3,5} N(A)=3

Maka,

P(A)=N(A)/N(S)

= 3/6

***

Nilai suatu peluang paling besar adalah 1 dan paling kecil adalah 0. Suatu kejadian yang pasti terjadi peluangnya adalah 1, sedangkan suatu kejadia yang tidak mungkin terjadi peluangnya adalah 0.

PELUANG KOMPLEMEN SUATU KEJADIAN

Jika peluang suatu kejadian A adalah P(A), maka peluang kejadian bukan A adalah P(A') = 1 - P(A).

Contoh: Jika peluang hari ini akan turun hujan adalah 1/3, maka peluang hari ini tidak hujan adalah?

Jawab: 1-1/3=2/3.

MATEMATIKA XI IPA SEMESTER I (lenny marlika)